
【対策すれば簡単!!】玉手箱・計数問題の解法テクニックを一挙公開
2022年10月17日更新
はじめに
「玉手箱の計数問題って、どんなのですか?」
「計数問題を見ただけでアレルギー!!」
「計数問題で何か簡単な解き方はないですか?」
数学や計算問題が苦手な人にとって、玉手箱の計数問題を見るだけで、身の毛がよだちますよね。
でも、安心してください。
計数問題は「記憶問題」です。
何の記憶問題かというと、「解答パターンの記憶問題」です。
解法パターンさえ記憶しておけば、いとも簡単に解ける問題ばかりなので、気を楽にしてください。
しかも、玉手箱の計数の問題形式は、大きく3つしかありません。
そういう意味では、的が絞りやすく対策を講じやすいので、光明を見出せますよね。
本記事では玉手箱の計数問題の全体的な形式を確認したうえで、3つの問題形式「四則逆算」「図表の読み取り」「表の空欄推測」の解法テクニックを公開していきます。
読後感として、「歴史の記憶問題と同じで、覚えておけば答えられる」という自信がみなぎってくるはずです。
10分ぐらいで、その記憶すべき解法テクニックが入手できますので、最後まで一気にお読みくださいね。
4泊5日の上京就活を応援!満員御礼の就活イベントを今年も開催!
宿泊費完全無料、東京までの交通費補助で負担を減らせます!
最大25社の優良成長企業と就活仲間に出会えるので、今から就活する学生は必見です!
あきらめないで!25卒も優良企業に出会えるチャンス!
夏採用に動き出す首都圏の優良企業を、就活ハンドブック独自にご紹介!
次こそうまく進めたい就活生に、専任のキャリアアドバイザーがつきます。
ぜひ、いまの不安をぶつけてみてください!
二人三脚で就活をサポートするので、就活をやってこなかった人も必見です!
1.玉手箱・計数の問題形式と出題パターン
見ての通り、時間の割りに問題数が多いのが玉手箱の特徴で、短時間で素早く問題を解く能力が問われます。
| 出題形式 | 出題内容 | 問題数 | 時間 | 1問あたり解答時間 |
| 四則逆算 | 方程式の一部が▢になっていて、当てはまる数値を回答する | 50問 | 9分 | 10.8秒 |
| 図表の読み取り | 図表に書いてある数値を読み取り、正しい選択肢を選択する | 29問 or 40問 | 15分 or 35分 | 31.0秒 or 52.5秒 |
| 表の空欄推測 | 表の一部に空欄があり、空欄にあてはまる数値を表全体から推測する | 20問 or 35問 | 20分 or 35分 | 60秒 or 60秒 |
ただし、3つの出題形式全部が出るわけではなく、「四則逆算」「図表の読み取り」「表の空欄推測」の3つの中から1つ出題されます。
たとえば、計数の試験で最初の問題が「図表の読み取り」であれば、以降は「図表の読み取り」の問題しか出ないということです。
とはいえ、企業側がどれを選択するかわからないので、すべての出題形式の対策を講じておく必要があります。
ただ、問題形式は最大で3個しかないので、的を絞れて対策しやすいWEBテストですね。
【言語/非言語/英語完全網羅】
SPI初心者でも短期間で対策できる資料配布中!
SPIなどの適性検査に自信がない学生は多いでしょう。
「何を勉強したらいいのか…」「どんな問題が出るか知りたい」そんな学生のためにまとめたものがSPI頻出問題集です。
SPIの出題範囲である言語/非言語/英語といった問題を完全網羅しています。
この問題集を解けば、一気に自信がつき内定へと近づくこと間違いなしです。
この機会にぜひ、問題集を解いて対策しておきましょう。
2.「四則逆算」の問題例と解法テク
それでは、実際の問題を使って解法テクニックを見ていきます。
まず初めに「四則逆算」の問題を見ていきましょう。
「四則逆算」は50問を9分で解く問題なので、1問あたり10秒で効率よく解く必要があります。
例1) 182+▢=312-92
▢をXと置くと、
182+X=312-92 → X=312-92-182=38
自宅受験型だと電卓を用意しておけば、計算スピードが加速するので重宝します。
センター会場の場合は筆算のスピード化が課題になりますね。
もう1問見ていきましょう。
例2) 24×36=27×▢
この解法テクは、▢=Xと置いて計算するやり方と、素因数分解で解くやり方があるので、どちらかスピードの早いほうを選択するといいでしょう。
→▢=Xのやり方
24×36=27X→X=24×36÷27=32
→素因数分解のやり方
24=2×2×2×3
36=2×2×3×3
24×36=2^5×3^3
一方で、27=3^3なので、除すると2^5が残り、答えが32に確定します。
例3)▢+272=▢×69
それでは最後の例を見てみましょう。
▢+272=▢×69
▢=Xと置くと、
X+272=69X
X(69-1)=272
68X=272
X=4
難易度は中学レベルなので、そこまで難しくはないと思います。
練習問題を5問用意しておきますので、さっそく解法テクを使って腕試ししてみましょう。
| ①68×▢=268+▢ ➁120÷8=▢÷3 ③4÷▢=24.5÷4.9 ➃6÷7=8×▢÷28 ➄8-20÷▢=4 |
【答え】
①4、➁45、③0.8、➃3、➄5
四則逆算については、以下の記事で詳しく紹介しています。もっと知りたい方はこちらもご確認ください。
3.「図表の読み取り」の問題例と解法テク
例1)ダムの年間取水量を100とすると、井戸水の年間取水量はどのように表示されるか。
年間取水量 158.9㎥
| 区 分 | 割 合 |
| ダ ム | 43.8% |
| 河川水 | 25.7% |
| 井戸水 | 21.3% |
| その他 | 9.3% |
ダムの年間取水量を100とすると、井戸水の年間取水量Xは以下の等式で導き出せますね。
43.8:21.3=100:X
X=48.6
例2) 2001年の研究費支出額が247億円のとき、対前年度比増加額率はおよそ何%か。
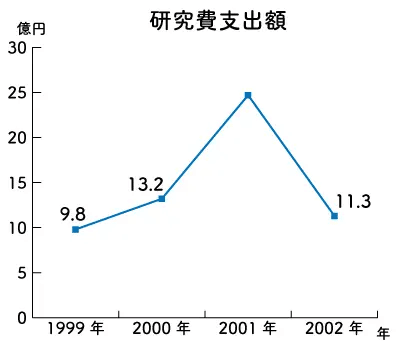
この問題の落とし穴は、「単位」です。
一見、2000年の研究費支出額は13.2億円に見えますが、2001年の研究費支出額が247億円なので、単位が10億円であることが読み取れます。
これを読み取れないとその場でアウトなので、慎重に吟味することが大切です。
したがって、2000年の研究費支出額が132億円となり除すると、
247÷132=1.871
になります。
ここでもう1つ落とし穴があり、増加率をそのまま187.1%とするとアウトです。
この1.871は2000年を1としたときの2001年の割合であるので、2000年分の1を引くことで増加率が算出できます。
つまり、
1.871-1=0.871→87.1%
が求める増加率となるわけです。
この2つの例題で、図表の読み取りの攻略ポイントが見えてきます。
【図表の読み取りの攻略ポイント】
| ① どの値が基準になるかを把握する ② 単位に注意する |
図表の読み取りでは、「何%か」「何倍か」「一方をXとしたときの、もう一方はどのように表せるか」といった表現で聞かれますが、要は「何倍か」を色々な表現を使って聞いているに過ぎません。
この「何倍か」は2つの値を除することで算出できますが、ここで大切なことは
「どちらの値が基準になるかを判断すること」
です。
たとえば、「A工場の人件費はB工場の人件費の何倍か」という問題が出題された場合、B工場の人件費の何倍かが問われているので、B工場が基準となり「A工場÷B工場」という算式で計算することにより、答えにたどり着けます。
逆の場合だと、その時点でアウトなので注意が必要ですね。
また、例題2が特異な例ですが、時間に追われると、焦った心理状態の中で、ついつい早とちりして「単位」を見誤り、間違いを連発するなんてこともあります。
「単位」を確認する癖を日頃の練習から徹底することで、このような過ちを回避できますね。
4.表の空欄の推測の問題例と解法テク
例1) ある会社でゴルフ場の芝張り工事の見積金額を検討しています。
【芝張り工事見積金額の一覧】
| 山岳GC | 森林CC | 湖畔GC | |
| 芝張り面積(坪) | 10,000 | 7,000 | 8,000 |
| 芝生単価(円/坪) | 4,000 | 6,000 | 5,500 |
| 養生材単価(円/坪) | 500 | 500 | 1,000 |
| 見積金額(万円) | 5,100 | 4,970 | ? |
湖畔GCの芝張り工事の見積金額はいくらと推定できるか?
これは完全なヒッカケ問題です。
私自身も引っ掛かりました(汗)
通常、この表の中にある要素で問題を解こうと思うので、早合点して湖畔GCの見積金額を
(0.55+0.1)×8,000=5,200万円
と計算してしまいそうですよね。
でも、この方法で山岳GCを検算すると、
(0.4+0.05)×10,000=4,500万円
となり、見積金額の5,100万円と異なり、「???」となるわけです。
そこで、この見積額をよく見てみると、
「芝生単価」と「養生単価」は、いずれも材料費なんですね。
ここに落とし穴があって、芝張りの人件費がこの表から欠落しているんです。
これを見極められるかどうかがカギなんですが、分からないなら、その時点で撃沈というわけです。
山岳GCを例にすると、
見積金額-材料費の見積金額=5,100-4,500=600万円
の差額があり、これが人件費だと分かります。
山岳GCの坪面積は10,000坪なので、
坪あたり人件費=600万円÷10,000坪=0.06万円/坪
となります。
このやり方で森林CCの坪あたり人件費単価を弾くと、
坪あたり人件費=4,970-((0.6+0.05)×7,000)÷7,000=0.06万円
なので、「坪あたり人件費は0.06万円」で間違いないことが確認できました。
したがって、この人件費を湖畔GC(8,000坪)に当てはめると
人件費=0.06×8,000=480万円
になります。
先ほど計算した材料費を加えると見積額は、
見積額=材料費+人件費=5,200+480=5,680万円
が答えということになりますね。
もう1つ例題を見ていきましょう。
例2)ある水族館の3日間の収入について、まとめています。
| 9月1日 | 9月2日 | 9月3日 | ||
| 入場者数(人) | 大 人 | 650 | 720 | 690 |
| 子 供 | 780 | 870 | 720 | |
| 天 気 | 曇り | 晴れ | 晴れ | |
| 動物園の入場券収入(万円) | 100.5 | 120.8 | 115.6 | |
| 土産店の収入(万円) | 14.5 | 15.7 | 13.2 | |
| レストラン収入(万円) | 20.8 | 23.4 | 17.9 | |
| 総収入(万円) | 181.3 | 210.3 | ? | |
9月3日の総収入はいくらだと思いますか?
まずこの表に記載されている収入に関わる項目を見ると、
・入場者数
・動物園の入場券収入
・土産店の収入
・レストラン収入
・総収入
が確認できます。
そこで、9月1日の動物園の入場券収入+土産店の収入+レストラン収入を計算すると、
100.5+14.5+20.8=135.8万円
なので、総収入の「181.3万円」に対して「45.5万円」届かないことが分かります。
同じように、9月2日も計算してみると、
120.8+15.7+23.4=159.9万円
となり、総収入「210.3万円」に「50.4万円」不足していることが見て取れます。
ここで「何かが抜けている」という疑問を持ち、それを見つけ出す作業が必要になります。
それが分からない場合は、この段階でアウトです。
設問では「水族館の収入」と書いてあるので、
「水族館の入場料が入ってない」
と気付くことが解法の糸口になります。
ただし、ここで「大人の料金と子供の料金は当然違うんだろうな」と頭のいい人ほど類推してしまうんですよね。
玉手箱特有のポイントですが、表の推測では大人と子供の入場料をそれぞれ計算させるほど、複雑な問題はまず出ません。
そのため、子供の入場料は0円と捉えて、大人の入場料のみを計算してみます。
先ほど計算した9月1日の不足額の「45.5万円」を大人の入場数「650人」で除します。
45.5÷650=0.07
ちなみに検算のため9月2日も計算してみると、
50.4÷720=0.07
になり、大人の入場料が「0.07万円(=700円)」で見合うことが分かります。
したがって、9月3日の大人の入場者数は「690人」なので、入場料収入は
0.07×690=48.3万円
となるわけです。
そこから9月3日の総収入を計算すると、
総収入=水族館入場料+動物園の入場券収入+土産店の収入+レストラン収入
=48.3+115.6+13.2+17.9=195万円
となるわけです。
この例題を見ても、玉手箱独特のパターンがありますので、例題を数多くこなしておかないと対応できないことが分かりますね。
最後にもう1つ例題を見ていきましょう。
例3)以下の表はあるサークルの学生数の推移を集計しています。
(単位:人)
| 2016年 | 2017年 | 2018年 | 2019年 | 2020年 | |
| 法 学 部 | 78 | 68 | 64 | 74 | 76 |
| 経済学部 | 36 | 16 | 48 | 58 | 70 |
| 商 学 部 | 46 | 36 | 32 | 44 | 22 |
| 文 学 部 | 40 | 30 | 36 | 44 | ? |
2020年の文学部の学生は何人と推測できるか?
まず全体人数を出していきます。
2016年の場合は、
法学部+経済学部*商学部+文学部=78+36+46+40=200
全体人数から文学部の割合を見ていくと、
40÷200=0.2=20%
というのがわかります。
同じように2017年を見ても、
30÷150=0.2=20%
だということがわかりました。
この辺りで、全体人数の20%を文学部に充てていると推測できますので、引き続き2018年、2019年で確認していきます。
2018年:36÷180=0.2=20%
2019年:44÷220=0.2=20%
で、全体数の20%を文学部に割り当てているという妥当性を掴めました。
したがって、2020年も全体数の20%で文学部の人数を算定すればいいわけです。
文学部の人数をXと置くと、
全体人数=76+70+22+X
また、文学部の学生数は全体の20%であることより、文学部の学生の5倍の人数が全体人数であることより、
全体人数=20X
と表せます。
したがって、
76+70+22+X=20X
となります。
これを解いていくと、
X=42
つまり、文学部の学生数が42人であることが推測されます。
いかがだったでしょうか?
今回の例題を通じて、下記の3ステップで解くことが効率的な解法だということもわかりましたね。
【表の空欄推測を解く3ステップ】
| ステップ1:ヒントとなる項目名を確認 ステップ2:表のある項目と他の項目が比例(反比例)の関係にないかを考える ステップ3:表のある項目と他の項目が足す・引く・掛ける・割るの関係にないかを考える |
まずステップ1として、
玉手箱の空欄推測問題では、表の項目名がヒントになります。
したがって、「何についての表なのか」を全体的に把握するために、表の項目についてチェックする癖付けをしましょう。
そのうえで、ステップ2で
表のある項目と他の項目は比例(反比例)の関係になっている場合が多いです。
なので、「?」を解く場合は、「?」と他の項目に比例(反比例)する関係はないかチェックしてください。
そして、ステップ3は、
比例(反比例)でなかった時の対処法です。
項目同士を加減乗除して、関係が成り立たないかを推論しましょう。
【言語/非言語/英語完全網羅】
SPI初心者でも短期間で対策できる資料配布中!
SPIなどの適性検査に自信がない学生は多いでしょう。
「何を勉強したらいいのか…」「どんな問題が出るか知りたい」そんな学生のためにまとめたものがSPI頻出問題集です。
SPIの出題範囲である言語/非言語/英語といった問題を完全網羅しています。
この問題集を解けば、一気に自信がつき内定へと近づくこと間違いなしです。
この機会にぜひ、問題集を解いて対策しておきましょう。
5.おわりに
本記事では玉手箱の計数問題に特化して、計数問題の構成や問題を例示しながら解法テクニックを公開してきました。
冒頭でもお話したとおり、問題を見た瞬間に、いかに素早くパターン認識できるかが「カギ」となります。
パターン認識できなければ、無間地獄のようにグルグルと彷徨いますが、パターン認識できれば、絡まった糸を解きほぐすようにスラスラと解いていくことが可能になります。
本記事の解法テクニックが玉手箱の計数問題の得点アップに貢献できれば、幸いです。
今回も最後までお読みいただき、ありがとうございました。玉手箱を攻略するため、アプリの活用など以下の記事で紹介するものもおすすめです。ぜひこちらの記事もご覧ください。
【期間限定公開!】就活のプロが
自己分析のやり方を徹底解説!
今回、期間限定で就活のプロフェッショナルであるキャリアアドバイザーが、エントリーシートや面接に悩んでる学生に向けて、だれでも簡単に自己分析が出来る方法を3つ紹介しました!
すぐに実行に移せるものばかりなので、ぜひ読んでみてください!















